Mastering the Diamond Problem: How C3 Linearization Solves Inheritance Ambiguities in Python
Deep Dive: Unraveling the Diamond Problem and C3 Linearization in Python

TL;DR: Use the .mro() method to determine the order in which methods are resolved in a multiple inheritance hierarchy.
Understanding Method Resolution Order (MRO) in Python’s Multiple Inheritance
When working with object-oriented programming (OOP), particularly in languages like Python that support multiple inheritance, it is crucial to understand which method will be called when there are overlapping function names across different classes.
This is where Method Resolution Order (MRO) comes in—it defines the order in which Python searches for a method in the class hierarchy. In simple cases, MRO is straightforward, but when dealing with complex inheritance structures, it can become difficult to predict which method will execute.
Python provides a built-in method, .mro(), which helps developers inspect the exact order in which Python will look for methods. This is especially useful in large-scale projects where deeply nested inheritance chains can introduce unexpected behavior.
The Evolution of MRO in Python
Earlier versions of Python (before 2.3) used a non-monotonic method resolution order. This meant that in some cases, Python could return inconsistent or ambiguous results when resolving methods. The problem was highlighted in a discussion by Samuele Pedroni on the Python development mailing list, where he pointed out cases where the resolution order was unpredictable and could lead to hard-to-debug issues.
Before Python 2.3, it was possible to create ambiguous inheritance hierarchies, leading to unexpected behavior. Consider the following example, which executes successfully in Python 2.2:
class A(object):
def method(self):
print "A"
class B(A):
def method(self):
print "B"
super(B, self).method()
class C(B, A):
def method(self):
print "C"
super(C, self).method()
C().method()Despite C inheriting from both B and A, Python 2.2 does not enforce a strict method resolution order (MRO), allowing potentially inconsistent hierarchies.
root@fda1e422ff26:/Python-2.2# python test.py
C
B
ATo address this, Python 2.3 introduced the C3 Linearization algorithm, which ensures:
Monotonicity (the order remains consistent across hierarchies).
A deterministic resolution order that prevents ambiguous hierarchies.
Predictability, making multiple inheritance safer to use.
This prevents ambiguous inheritance structures like the following:
class A:
def method(self):
print('A')
class B(A):
def method(self):
print('B')
super().method()
class C(A, B):
def method(self):
super().method()
print('C') class C(A, B):
^^^^^^^^^^^^^^^
TypeError: Cannot create a consistent method resolution
order (MRO) for bases A, BWhy MRO Matters
In modern Python (3.x), the C3 Linearization (also known as the "C3 superclass linearization") is used to determine method resolution. This ensures that:
Subclasses come before parent classes in the order.
Multiple parents are resolved in the order they are listed in the class definition.
If a class appears multiple times in the hierarchy, it is only considered once (no duplication).
The Diamond Problem and How C3 Linearization Solves It
In multiple inheritance, the diamond problem arises when a class inherits from two classes that both inherit from a common superclass. This can create ambiguity in method resolution. C3 Linearization (also known as MRO - Method Resolution Order) provides a deterministic way to resolve this issue.
Let’s analyze the following example:
Python Code:
class One(metaclass=Typer):
def show(self):
print("One")
class Two(One):
def show(self):
print("Two")
class Three(One):
def show(self):
print("Three")
class Four(Three, Two):
def show(self):
super().show()
print("Four")
Four().show()
print(Four.mro())Class Inheritance Diagram:
Typer (metaclass)
│
┌───┴───┐
│ │
One (other classes using Typer)
/ \
/ \
Two Three
\ /
\ /
Four
What Will Be the Output?
Since Four.show() calls super().show(), the method resolution follows C3 Linearization to determine the method order.
How C3 Linearization Works:
C3 Linearization follows this rule:
L[C] = C + merge( L[Parent1], L[Parent2], ..., List of Parents in order)
Where L[C] represents the method resolution order of class C.
Compute L[One] (Base class):
L[One] = [One, object]Compute L[Two] and L[Three]:
L[Two] = [Two] + L[One] = [Two, One, object] L[Three] = [Three] + L[One] = [Three, One, object]Compute L[Four] using C3 Merge:
L[Four] = [Four] + merge(L[Three], L[Two], [Three, Two])Step 1: Pick the first valid head from
L[Three],L[Two], and[Three, Two].Threeis the first head and is not in the tail of any other list, so we pickThree.
L[Four] = [Four, Three] + merge([One, object], [Two, One, object], [Two])Step 2: The next valid head is
Two.
L[Four] = [Four, Three, Two] + merge([One, object], [One, object])Step 3: The next valid head is
One, followed byobject:L[Four] = [Four, Three, Two, One, object]
Final Method Resolution Order (MRO)
[Four, Three, Two, One, object]The exmaple might seem trivial and make thing more complicated than it should, but in secenraio whee there are many inheretes it shines and make
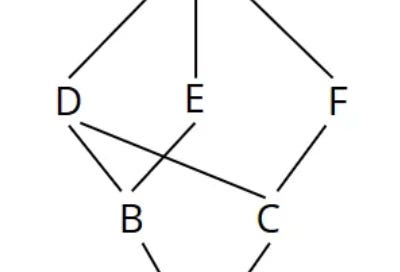
class F(O):pass
class E(O):pass
class D(O):pass
class C(D,F):pass
class B(D,E):pass
class A(B,C):passWhere O is the base object class.
What is L[A]? It’s tough to predict directly.
Let’s go step by step.
L[A] = A + merge (L[B], L[C], BC)
We need L[B] and L[C] to calculate this.
L[B] = B + merge( DO, EO, DE)
L[B] = BD+ merge( O, EO, E) # head =D
L[B] = BD + merge( O, EO, E) # head =O, not a good head
L[B] = BDE + merge( O, O) # head =E
L[B] =BDEO # head =O
and
L[C] = C + merge( DO, FO, DF)
L[C] = CD + merge( O, FO, F) # head=D
L[C] = CD+ merge( O, FO, F) # head=O, not a good head
L[C] = CDF+ merge( O, O ) # head=F
L[C]= CDFO # head =O
So now substituting L[B] and L[C]
L[A] = A +merge( BDEO, CDFO, BC)
L[A] = AB +merge( DEO, CDFO, C) # head =B
L[A] = AB +merge( DEO, CDFO, C) # head =D, not a good head because it is in tail of CDFO
L[A] = ABC +merge( DEO, DFO) # head =C
L[A] = ABCD +merge( EO, FO) # head =D
L[A] = ABCDE +merge( O, FO) # head =E
L[A] = ABCDEF +merge( O, O) # head =F
L[A] = ABCDEFO # head =O
So MRO is A->B->C->D->E->F->O
C3 provides a solution only when a monotonic order exists.